How a student becomes a teacher: learning and forgetting through Spectral methods
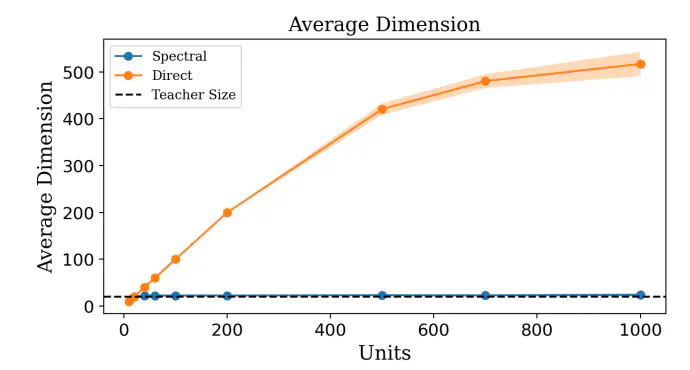We test the performance of a novel pruning strategy grounded on the inspection of the eigenvalues magnitude at the end of the training. The method is applied to a fully connected network trained on tasks of increasing complexity. When the complexity of the function is known we are capable of pruning the network to a stable minimal substructure, which is able to perform the task with the same accuracy of the full network.Abstract
In theoretical Machine Learning, the teacher-student paradigm is often employed as an effective metaphor for real-life tuition. A student network is trained on data generated by a fixed teacher network until it matches the instructor’s ability to cope with the assigned task. The study proposes a novel optimization scheme building on a spectral representation of linear transfer of information between layers. This method enables the isolation of a stable student substructure, mirroring the teacher’s complexity in terms of computing neurons, path distribution, and topological attributes. Pruning unimportant nodes based on optimized eigenvalues retains full network performance, illustrating a second-order phase transition in neural network training.
Lorenzo Giambagli
PostDoc Department of
Biophysics & AI4
My research interests include Spectral analysis of Deep Neural Network (DNN), Structura Pruning, Bayesian Inference in DNN, Simplicial Complexes Dynamics, Theoretical Neuroscience