Machine learning in spectral domain

Abstract

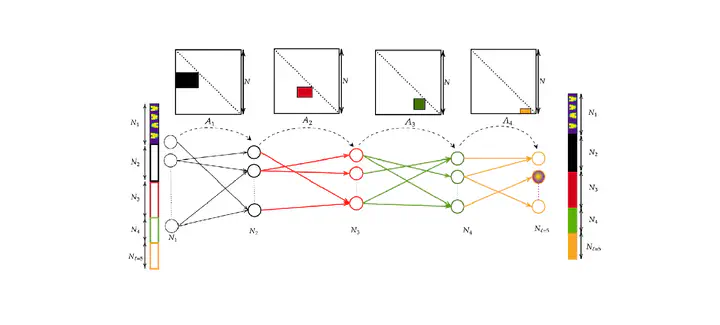
Deep neural networks are usually trained in the space of the nodes, by adjusting the weights of existing links via suitable optimization protocols. We here propose a radically new approach which anchors the learning process to reciprocal space. Specifically, the training acts on the spectral domain and seeks to modify the eigenvalues and eigenvectors of transfer operators in direct space. The proposed method is ductile and can be tailored to return either linear or non-linear classifiers. Adjusting the eigenvalues, when freezing the eigenvectors entries, yields performances that are superior to those attained with standard methods restricted to operate with an identical number of free parameters. To recover a feed-forward architecture in direct space, we have postulated a nested indentation of the eigenvectors. Different non-orthogonal basis could be employed to export the spectral learning to other frameworks, as e.g. reservoir computing.

Lorenzo Giambagli

PostDoc Department of Physics, Freie Universität Berlin

My research interests include Spectral analysis of Deep Neural Network (DNN), Structura Pruning, Bayesian Inference in DNN, Simplicial Complexes Dynamics, Theoretical Neuroscience