Training of sparse and dense deep neural networks: Fewer parameters, same performance

Abstract

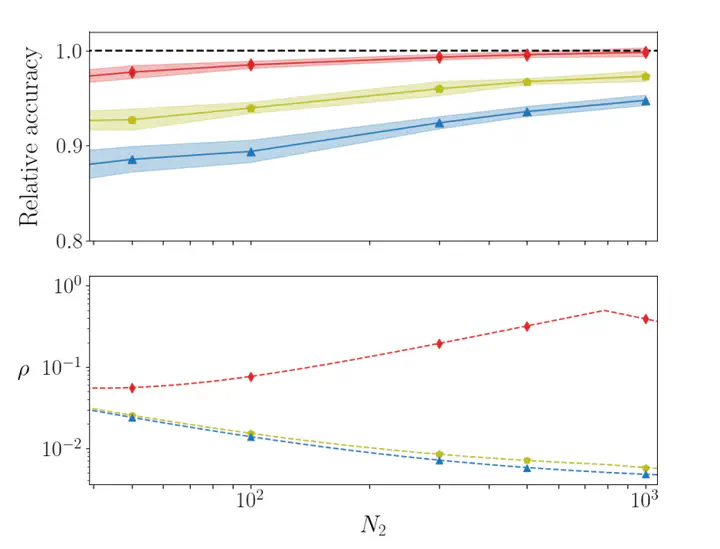
Deep neural networks can be trained in reciprocal space by acting on the eigenvalues and eigenvectors of suitable transfer operators in direct space. Adjusting the eigenvalues while freezing the eigenvectors yields a substantial compression of the parameter space. This latter scales by definition with the number of computing neurons. The classification scores as measured by the displayed accuracy are, however, inferior to those attained when the learning is carried in direct space for an identical architecture and by employing the full set of trainable parameters (with a quadratic dependence on the size of neighbor layers). In this paper, we propose a variant of the spectral learning method as in Giambagli et al. [Nat. Commun. 12, 1330 (2021)], which leverages on two sets of eigenvalues for each mapping between adjacent layers. The eigenvalues act as veritable knobs which can be freely tuned so as to (1) enhance, or alternatively silence, the contribution of the input nodes and (2) modulate the excitability of the receiving nodes with a mechanism which we interpret as the artificial analog of the homeostatic plasticity. The number of trainable parameters is still a linear function of the network size, but the performance of the trained device gets much closer to those obtained via conventional algorithms, these latter requiring, however, a considerably heavier computational cost. The residual gap between conventional and spectral trainings can be eventually filled by employing a suitable decomposition for the nontrivial block of the eigenvectors matrix. Each spectral parameter reflects back on the whole set of internode weights, an attribute which we effectively exploit to yield sparse networks with stunning classification abilities as compared to their homologs trained with conventional means.

Lorenzo Giambagli

PostDoc Department of Physics, Freie Universität Berlin

My research interests include Spectral analysis of Deep Neural Network (DNN), Structura Pruning, Bayesian Inference in DNN, Simplicial Complexes Dynamics, Theoretical Neuroscience