Spectral Deep Learning

Understanding Deep Neural Networks through the lens of Spectral Theory of Graph and Dynamical Systems.

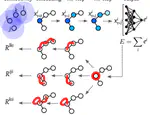
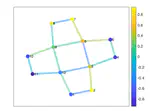
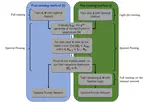
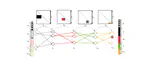
My research in deep learning addresses a seemingly simple yet profoundly impactful question: Can a neural network be envisioned as a graph with neurons as nodes and connections as links? More specifically, is it feasible to spectrally analyze the adjacency matrix of this graph? The affirmative answer to this question has profound implications, allowing the connections within the network to be described through the eigenvectors and eigenvalues of the graph’s adjacency matrix. This spectral perspective has facilitated two significant advancements:

Eigenvalue Inspection: By examining the eigenvalues before and/or after training, we gain insights into which nodes (neurons) play crucial roles in the network’s functionality. This understanding has been pivotal in developing Structural Pruning techniques, which enhance the network’s efficiency and performance by selectively removing less significant nodes.
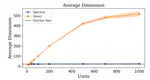
Dynamic Learning Process Reformulation: This approach has led to the creation of advanced recurrent networks. These networks are not static; they learn and adapt by dynamically modifying the attractors’ basins of attraction based on predefined criteria. This adaptive quality allows the networks to learn functions or classes more effectively, showcasing a remarkable flexibility in their learning capability.

I also have some applied works and more theoretical ones going on, follow me for new papers on the subject!

Related Publications

How a student becomes a teacher: learning and forgetting through Spectral methods

This study explores the teacher-student paradigm in machine learning, focusing on overparameterized student networks trained by fixed teacher networks. It introduces a new optimization scheme using spectral representation of linear information transfer between layers. This approach allows identifying a stable student substructure that mirrors the teacher’s complexity. The method shows that pruning unimportant nodes, based on optimized eigenvalues, does not degrade performance, indicating a second-order phase transition with universality traits in neural network training.

Lorenzo Giambagli, Lorenzo Buffoni, Lorenzo Chicchi, Duccio Fanelli

How a student becomes a teacher: learning and forgetting through Spectral methods

A Bridge between Dynamical Systems and Machine Learning: Engineered Ordinary Differential Equations as Classification Algorithm (EODECA)

EODECAs, merging machine learning with dynamical systems, enhance interpretability and transparency in neural networks. They employ continuous ordinary differential equations, offering both high classification accuracy and an understanding of data processes, addressing the opacity of traditional deep learning models. This approach signifies a step towards more comprehensible machine learning models.

Raffaele Marino, Lorenzo Giambagli, Lorenzo Chicchi, Lorenzo Buffoni, Duccio Fanelli

Complex Recurrent Spectral Network

The Complex Recurrent Spectral Network (C-RSN) is a novel AI model that more accurately mimics biological neural processes using localized non-linearity, complex eigenvalues, and separated memory/input functionalities. It demonstrates dynamic, oscillatory behavior akin to biological cognition and effectively classifies data, as shown in tests with the MNIST dataset.

Lorenzo Chicchi, Lorenzo Giambagli, Lorenzo Buffoni, Raffaele Marino, Duccio Fanelli

Complex Recurrent Spectral Network

Global topological synchronization on simplicial and cell complexes

This research explores the global synchronization of topological signals on higher-order networks, revealing that topological constraints impact synchronization differently across various network structures.

Timoteo Carletti, Lorenzo Giambagli, Ginestra Bianconi

Global topological synchronization on simplicial and cell complexes

Non-parametric analysis of the Hubble Diagram with Neural Networks

This study introduces a neural network-based method for nonparametric analysis of the Hubble diagram, extended to high redshifts. Validated using simulated data, the method aligns with a flat Λ (Lambda) cold dark matter model (ΩM ≈ 0.3) up to z ≈ 1-1.5, but deviates at higher redshifts. It also suggests increasing ΩM values with redshift, indicating potential dark energy evolution.

Lorenzo Giambagli, Duccio Fanelli, Guido Risaliti, Matilde Signorini

Non-parametric analysis of the Hubble Diagram with Neural Networks

Recurrent Spectral Network (RSN): Shaping a discrete map to reach automated classification

The Recurrent Spectral Network (RSN) is a new automated classification method that uses dynamical systems to direct data to specific targets, demonstrating effectiveness with both a simple model and a standard image processing dataset.

Lorenzo Chicchi, Duccio Fanelli, Lorenzo Giambagli, Lorenzo Buffoni, Timoteo Carletti

Recurrent Spectral Network (RSN): Shaping a discrete map to reach automated classification

Diffusion-driven instability of topological signals coupled by the Dirac operator

This research examines reaction-diffusion processes on networks, particularly focusing on topological signals across nodes, links, and cells. It uses the Dirac operator to study interactions and reveals conditions for Turing pattern emergence, validating the findings on network models and square lattices.

Lorenzo Giambagli, Lucille Calmon, Riccardo Muolo, Timoteo Carletti, Ginestra Bianconi

Diffusion-driven instability of topological signals coupled by the Dirac operator

Spectral pruning of fully connected layers

Training neural networks in spectral space focuses on optimizing eigenvalues and eigenvectors instead of individual weights, allowing effective implicit bias that node enables pruning without sacrificing performance.

Lorenzo Buffoni, Enrico Civitelli, Lorenzo Giambagli, Lorenzo Chicchi, Duccio Fanelli

Spectral pruning of fully connected layers

Machine learning in spectral domain

We introduce a new method for training deep neural networks by focusing on the spectral space, rather than the traditional node space. It involves adjusting the eigenvalues and eigenvectors of transfer operators, offering improved performance over standard methods with an equivalent number of parameters.

Lorenzo Giambagli, Lorenzo Buffoni, Timoteo Carletti, Walter Nocentini, Duccio Fanelli

Machine learning in spectral domain

Mobility-based prediction of SARS-CoV-2 spreading

This paper analyzes the effectiveness of containment measures for SARS-CoV-2, using mobility data to gauge their impact. A deep learning model predicts virus spread scenarios in Italy, showing how these measures help flatten the infection curve and estimating the time required for their noticeable effects.

Lorenzo Chicchi, Lorenzo Giambagli, Lorenzo Buffoni, Duccio Fanelli

Training of sparse and dense deep neural networks: Fewer parameters, same performance

This study presents a variant of spectral learning for deep neural networks, where adjusting two sets of eigenvalues for each layer mapping significantly enhances network performance with fewer trainable parameters. This method, inspired by homeostatic plasticity, offers a computationally efficient alternative to conventional training, achieving comparable results with a simpler parameter setup. It also enables the creation of sparser networks with impressive classification abilities.

Lorenzo Chicchi, Lorenzo Giambagli, Lorenzo Buffoni, Timoteo Carletti, Marco Ciavarella, Duccio Fanelli

Training of sparse and dense deep neural networks: Fewer parameters, same performance